xのx乗

&mimetex(x^x);の謎

矛盾？†

&mimetex(0^x);の系列†

• &mimetex(0^4=0);
• &mimetex(0^3=0);
• &mimetex(0^2=0);
• &mimetex(0^1=0);
• &mimetex(0^0=?); すごく0になるっぽい

&mimetex(x^0);の系列†

• &mimetex(4^0=1);
• &mimetex(3^0=1);
• &mimetex(2^0=1);
• &mimetex(1^0=1);
• &mimetex(0^0=?); すごく1になるっぽい。

グラフ†

最小†

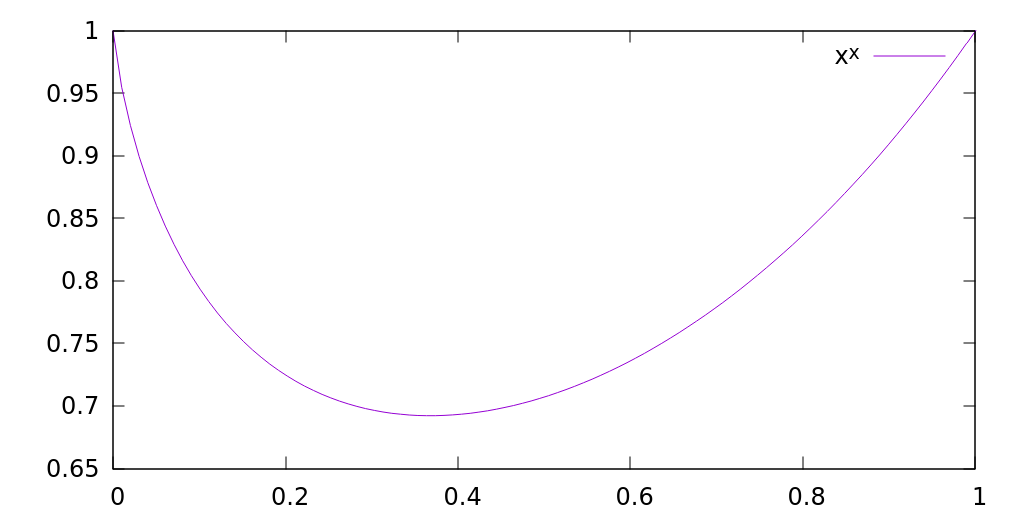
• 微分してみる。
• &mimetex(f(x)=x^x);

• &mimetex(\log{f(x)}=\log{x^x}=x\log{x});

• &mimetex(\frac{d}{dx}\log{f(x)}=\frac{d}{dx}x\log{x});

• &mimetex(\frac{d}{dx}\log{f(x)}=\frac{1}{f(x)}\frac{d}{dx}f(x)=1\log{x}+x\frac{1}{x}=\log{x}+1);

• &mimetex(\frac{d}{dx}f(x)=f(x)(\log{x}+1)=x^x(\log{x}+1));

• 微分した関数が0になるのは&mimetex(\log{x}=-1);のとき、つまり&mimetex(x=\frac{1}{e});

最小値のグラフ†

• 近似値として0.36787944117ぐらい

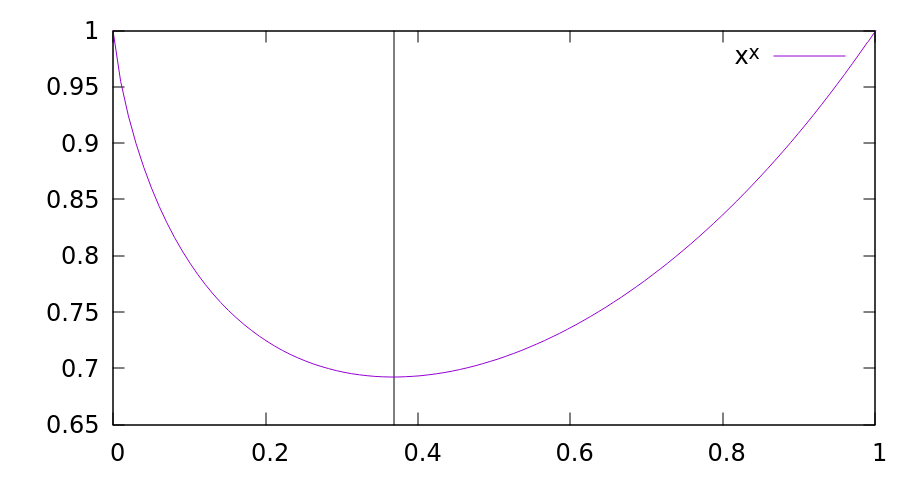
3次元のグラフ†

• &mimetex(z=x^y); のグラフを描いてみた

• このグラフのうち、&mimetex(y=x);の平面で切断したのが、直前の「最小値のグラフ」

• たしかに途中まで減少した後に増加に転じていることがわかる
• そして、4本の矢印を書き込んだが、グラフの断面が直線状になってるのに、x=y=0 の点から一周してもどってくると、もとの場所に戻らない、という不思議なグラフになっている。
• 単純なグラフなのにこんなことが起きるとは、数学は奥が深い

ジャンル:数学

最新の20件