東急沿線の公園を巡回するルート

元ネタはURBAN HACKS社さんの広告で、その広告を見かけたツイート

お題†

「東急沿線の素敵な公園を巡回する未来の乗り物の、最短周遊ルートは？」

概要†

• 無向グラフがあって頂点同士がいくつかのエッジで接続されている。 =それぞれのエッジには所要時間（コスト）があり、最短所要時間（最小コスト）を求める。
• なおルートは問題文中に「周遊」「巡回」とあるように、スタートの頂点に戻ってくる必要があり、また全ての公園を１回ずつ訪れる必要がある。
  • 経路はつまりハミルトン閉路である必要がある。
  • ハミルトン閉路 (Hamiltonian Cycle) とは、グラフの各頂点を1度ずつだけ訪れ、スタート地点に戻ってくる順回路のこと
• つまるところこの問題はセールスマン巡回問題なのである。
  • 自社から出発して全てのお客さんのところに訪問し、帰社するのに最短経路はどれか、というのがセールスマン巡回問題

解法1†

• 概要に書いた通り、セールスマン巡回問題なので良い解法はないと思い、とりあえず全探索してみた
  • 全探索した上で一番コストの少ない経路を調べてみた。
  • 順回路なのでスタート地点にこだわる必要は無い。そこは便利
  • 全探索と言えど、頂点10個ぐらいなので、NP困難と言えど普通に解ける。
• が、試してみたところ、順路は実質1つしか見つからなかった。
  • 厳密には1つの経路で、回る順序が2パターン
• というわけで、全探索するまでもなく、実はグラフとにらめっこするのが最善の策だと気づいた。

解法2†

• まず、このグラフを書き起こしたのが図1である
  • 各頂点のアルファベットはもとの問題と同じにしてある

図1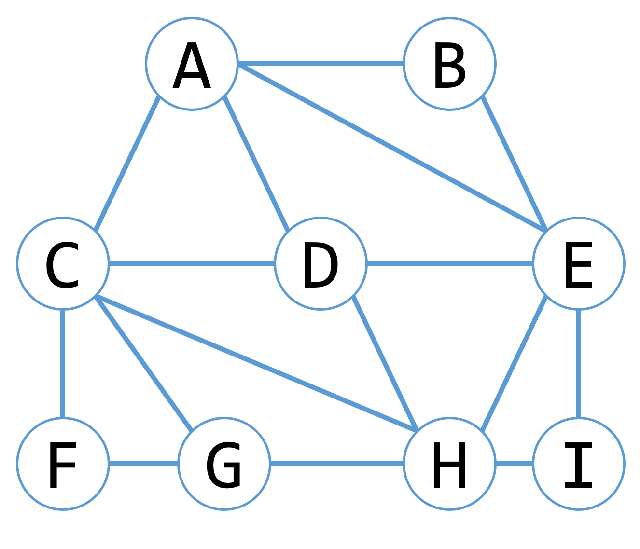

• このグラフのうち、「外側」と「内側」に分けた場合、いくつかのエッジはグラフの内側だけ通ることがわかる
  • 本当はグラフの外側と内側は厳密に話す必要があるのだけれど、問題のグラフは平面グラフでもあるため、エッジは「外側に接するか」「完全に内側を通るか」の2種類だけしか存在しない。
• 具体的には図2の二重線にした部分は「内側」を通るエッジである。

図2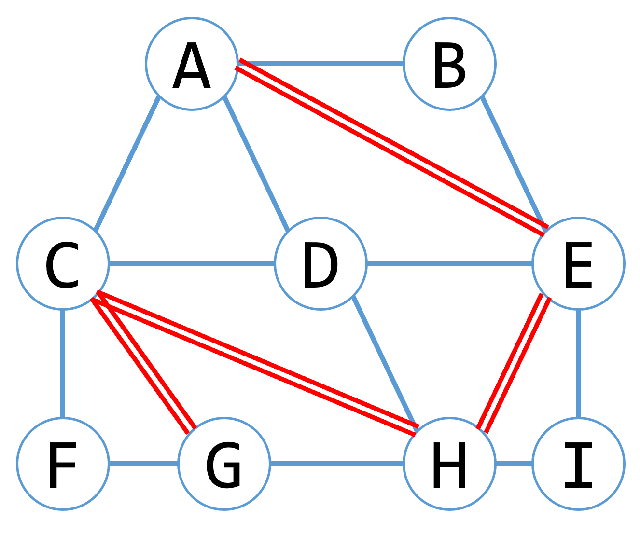

• さて、この内側のエッジを通った場合、困ったことがおきる。
• 説明のため、図3のようなグラフを使う。

図3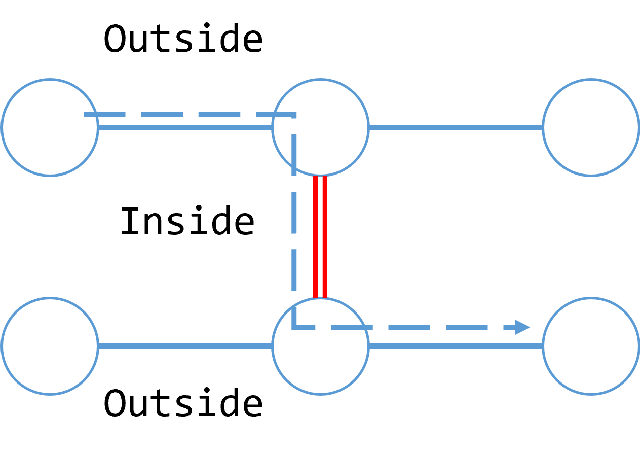

• 「内側」のエッジは必ず「外側」の頂点からつながるので、「内側のエッジ」を通る場合、図3の点線に示したように、

外側の頂点→内側のエッジ→外側の頂点

• と移動する必要がある。
• しかし、内側のエッジを通る際に通過した外側の頂点にはもう訪れることができないため、結果として「通った内側のエッジで、グラフを二分割」したことになってしまう。

内側のエッジを通るとグラフを二分割してしまう

• つまり、「内側のエッジ」は通ると問題が解決できなくなるため、内側のエッジを取り除いてグラフをシンプルにしてみる。
• それが図4である。

図4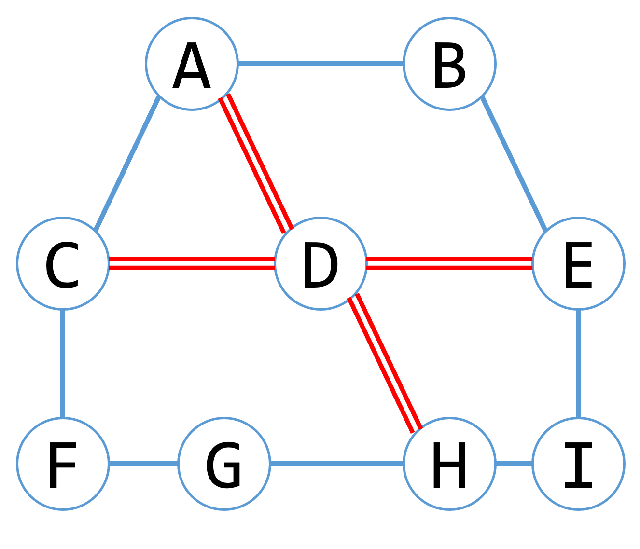

• さて、今度は内側の頂点とも言うべき、頂点Dに着目してみよう。（もとの問題だと碑文谷公園）
• この頂点Dには4本のエッジが接続されており、頂点Dに入ったあと出ていかないといけないので、頂点Dの入口と出口を選ぶことに相当する。
• つまり頂点Dを通る方法は　&mimetex("_4C_2");　で6通り存在する。
• 6通りのうち、2通りは前述の「内側のエッジ」と同じく、グラフを二分割してしまうため、取りうる選択肢は４つ
  • A-D-E
  • E-D-H
  • H-D-C
  • C-D-A
  • の４択となる。
  • なお、グラフは無向グラフなので逆順に通るパターンは同一とカウントする

• 今、頂点A、B、D、Eの4点で構成される部分グラフに着目しよう。
• 図5に部分グラフを示す

図5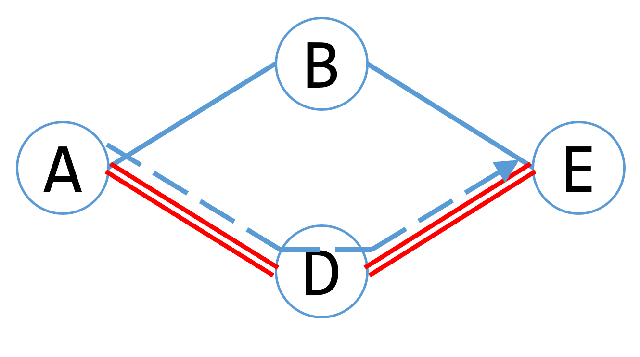

• この時、頂点AからEに抜けようとすると、頂点Bを通るか、頂点Dを通るかの2択となる。
• 繰り返しになるが、問題文ではハミルトン閉路が制約なので、

A→D→E→B→A

• みたいにAにまた戻ってくる場合は解答に適さない
• つまりA→D→E（図中の点線の経路）を通ってしまうと、頂点Bにたどり着くことができなくなり、解答に適さない
• よって、ここの部分グラフでは頂点A→B→E（あるいはその逆順）しか通る方法が認められない。

• もう一度図4を見ると頂点Dを通れる経路として頂点C→D→A（あるいはその逆順）しかないことがわかる。
• となると、ハミルトン閉路としてありうる経路は頂点Aを基準とすると

A→B→E→I→→H→G→F→C→D→A

• もしくはその逆順しかありえないことになる。
• というわけで、
  • 問題文は巡回セールスマン問題に見せかけて、
  • 実はハミルトン閉路問題で、
  • グラフをよく眺めれば計算機を使わずに問題が解けることを示した。

• なお、実際の所要時間は各自広告とにらめっこして計算してみてほしい。

:数学

最新の20件