100人の誕生日が重なる確率

有名な問題？

100人の生徒がいる．全員の誕生日を調べ，最低1組以上誕生日が重なる生徒が現れる確率を求めよ
(ただし，このクラスに2月29日生まれはいないものとする)

解法†

• 全員がばらばらの誕生日である確率を求める
• 問題は↑と背反の事象なので1から引けばよい
• n人の誕生日が全部ばらばらである確率を&mimetex(p\(n\));で表すと

• &mimetex(p\(1\)=1);

• &mimetex(p\(2\)=\frac{365}{365}\cdot\frac{364}{365});

• &mimetex(p\(3\)=\frac{365}{365}\cdot\frac{364}{365}\cdot\frac{363}{365});

• &mimetex(p\(n\)=\prod_{i=1}^{n}\frac{366-i}{365}=\frac{1}{365^n}\cdot\frac{365!}{(365-n)!});

• 答えは&mimetex(1-\frac{1}{365^n}\cdot\frac{365!}{(365-n)!});

解法(もし2月29日生まれがいたら)†

• いたとしても上記の式を365から366に(そして366を367に)書き換えれば基本的に同じ．
• 2月29日の存在確率が他の誕生日に比べ&mimetex(\frac{1}{4});だとしても基本的には同じ
• よっぽどミソなのはこれが予想外に高い確率でかぶるという結果．

実際の値†

• Gnuplotでプロットしてみた
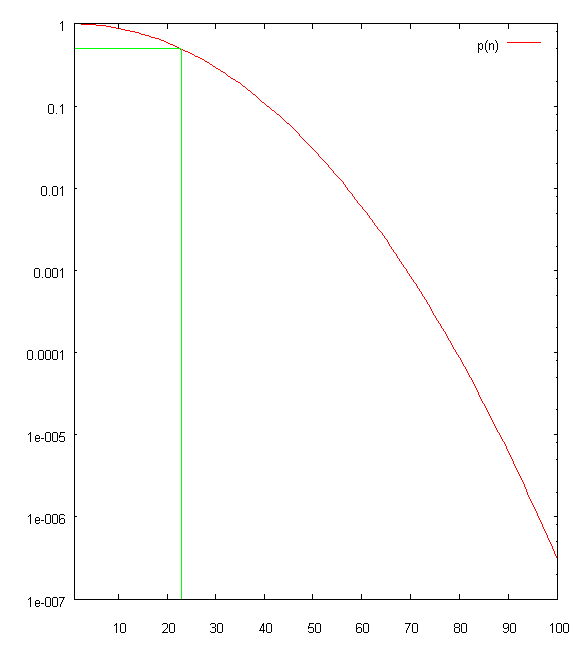
  • 緑の線はp(n)=0.5とn=23
  • 縦軸が対数軸になってるのに注目
• 数値

  n	&mimetex(p\(n\));	&mimetex(f\(n\));
  1	1	0
  10	0.861218	0.138782
  22	0.524304	0.475696
  23	0.492703	0.507297
  50	0.025638	0.974362
  70	0.000681	0.999319
  100	0.0000002	0.9999998*1

次のお題†

100人の生徒がいる．全員の誕生日を調べ，同じ誕生日の生徒が少なくとも3人重なる組が現れる確率を求めよ
(ただし，このクラスに2月29日生まれはいないものとする)

:数学

最新の20件